El Álgebra, rama fundamental de las matemáticas

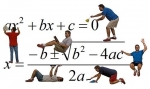
El Álgebra es una Rama de las Matemáticas en la que se usan letras para representar relaciones aritméticas. Al igual que en la aritmética, las operaciones fundamentales del álgebra son adición, sustracción, multiplicación, división y cálculo de raíces. La aritmética, sin embargo, no es capaz de generalizar las relaciones matemáticas, como el teorema de Pitágoras, que dice que en un triángulo rectángulo el área del cuadrado que tiene como lado la hipotenusa es igual a la suma de las áreas de los cuadrados cuyos lados son los catetos.

El álgebra clásica, que se ocupa de resolver ecuaciones, utiliza símbolos en vez de números específicos y operaciones aritméticas para determinar cómo usar dichos símbolos. El álgebra moderna ha evolucionado desde el álgebra clásica al poner más atención en las estructuras matemáticas. Los matemáticos consideran al álgebra moderna como un conjunto de objetos con reglas que los conectan o relacionan. Así, en su forma más general, se dice que el álgebra es el idioma de las matemáticas.

La historia del álgebra comenzó en el antiguo Egipto y Babilonia, donde fueron capaces de resolver ecuaciones lineales como (ax = b) y cuadráticas (ax2 + bx = c), así como ecuaciones indeterminadas como x2 + y2 = z2, con varias incógnitas. Los antiguos babilonios resolvían cualquier ecuación cuadrática empleando esencialmente los mismos métodos que hoy se enseñan.

Los matemáticos alejandrinos Herón y Diofante continuaron con la tradición de Egipto y Babilonia, aunque el libro Las aritméticas de Diofante es de bastante más nivel y presenta muchas soluciones sorprendentes para ecuaciones indeterminadas difíciles. En las civilizaciones antiguas se escribían las expresiones algebraicas utilizando abreviaturas sólo ocasionalmente; sin embargo, en la edad media, los matemáticos árabes fueron capaces de describir cualquier potencia de la incógnita x, y desarrollaron el álgebra fundamental de los polinomios, aunque sin usar los símbolos modernos.

Esta álgebra incluía multiplicar, dividir y extraer raíces cuadradas de polinomios, así como el conocimiento del teorema del binomio. El matemático, poeta y astrónomo persa Omar Khayyam mostró cómo expresar las raíces de ecuaciones cúbicas utilizando los segmentos obtenidos por intersección de secciones cónicas, aunque no fue capaz de encontrar una fórmula para las raíces.

A principios del siglo XVI los matemáticos italianos Scipione del Ferro, Tartaglia y Gerolamo Cardano resolvieron la ecuación cúbica general en función de las constantes que aparecen en la ecuación. Ludovico Ferrari, alumno de Cardano, pronto encontró la solución exacta para la ecuación de cuarto grado y, como consecuencia, ciertos matemáticos de los siglos posteriores intentaron encontrar la fórmula de las raíces de las ecuaciones de quinto grado y superior.

El foco de atención se trasladó de las ecuaciones polinómicas al estudio de la estructura de sistemas matemáticos abstractos, cuyos axiomas estaban basados en el comportamiento de objetos matemáticos, como los números complejos, que los matemáticos habían encontrado al estudiar las ecuaciones polinómicas. Dos ejemplos de dichos sistemas son los grupos y las cuaternas, que comparten algunas de las propiedades de los sistemas numéricos, aunque también difieren de ellos de manera sustancial.